向量叉乘 .cross()

threejs三维向量Vector3提供了叉乘的两个相关方法.crossVectors()和.cross()。

叉乘也有其它称呼，比如向量积、外积、叉积、矢积。

大学高等数学一般会介绍叉乘，如果你没有学习过，或者已经忘了，直接去查看百科关于叉乘 (opens new window)介绍，你可能也不知道在说什么，不过这没关系，咱们课程会用具体的threejs案例，让你从零掌握和理解抽象的数学概念叉乘。

已知两个向量a、b

已知3D空间中两个向量a、b

const a = new THREE.Vector3(50, 0, 0);
const b = new THREE.Vector3(30, 0, 30);

箭头可视化向量a、b

使用箭头THREE.ArrowHelper可视化表示向量。

//给箭头设置一个起点(随便给个位置就行)
const O = new THREE.Vector3(0, 0, 0);
// 红色箭头表示向量a
const arrowA = new THREE.ArrowHelper(a.clone().normalize(), O, a.length(),0xff0000);
// 绿色箭头表示向量b
const arrowB = new THREE.ArrowHelper(b.clone().normalize(), O, b.length(),0x00ff00);

向量叉乘方法.crossVectors()

先给大家解释下向量Vector3叉乘方法.crossVectors()的语法，然后再给大家解释叉乘的数学几何含义。

c.crossVectors(a,b)向量a和b叉乘的结果是一个新的向量c。

// 创建一个向量c，用来保存叉乘结果
const c = new THREE.Vector3();
//向量a叉乘b，结果保存在向量c
c.crossVectors(a,b);
console.log('叉乘结果',c);//叉乘结果是一个向量对象Vector3

可视化叉乘结果c

// 可视化向量a和b叉乘结果：向量c
const arrowC = new THREE.ArrowHelper(c.clone().normalize(), O, c.length()/30,0x0000ff);

这时候你会直观的发现向量c垂直于向量a、b构成的平面，或者说向量c同时垂直于向量a、向量b。

叉乘结果向量c几何含义

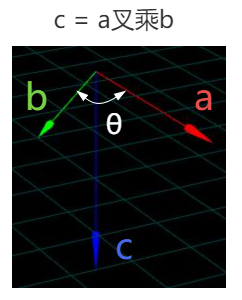
一方面是向量方向，刚刚通过可视化箭头给大家总结过，向量a叉乘向量b，得到一个新的向量c，向量c垂直于向量a和b构成的平面，或者说向量c同时垂直于向量a、向量b。

另一方面是向量长度，假设向量a和b的夹角是θ，a和b叉乘结果是c，c的长度c.length()是a长度a.length()乘b长度b.length()乘夹角θ的正弦值sin(θ)

c.crossVectors(a,b);
c.length() = a.length()*b.length()*sin(θ)

向量b叉乘向量a.crossVectors(b,a)

c.crossVectors(a,b);//a叉乘b
c.crossVectors(b,a);//b叉乘a

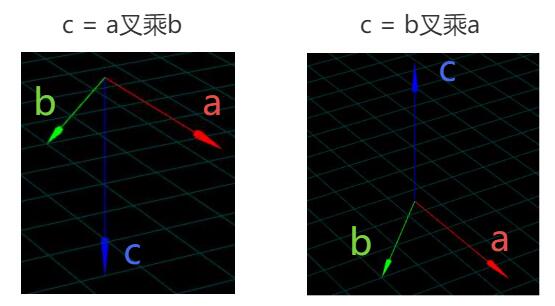
箭头可视化向量b叉乘ac.crossVectors(b,a)的结果，你会发现向量c与原来向量a叉乘bc.crossVectors(a,b)的方向反过来。

// 可视化向量b和a叉乘结果：向量c
new THREE.ArrowHelper(c.clone().normalize(), O, c.length()/30,0x0000ff);

总结：叉乘不满足交换律

你通过比较向量a叉乘b与向量b叉乘a区别，顺序不同结果不同，也就是说叉乘不满足交换律。

// a叉乘b
c.crossVectors(a,b);
// b叉乘a
c.crossVectors(b,a);

叉乘方向(右手螺旋定则判断)

首先明确一定，向量a、b叉乘，得到一个向量c，向量c垂直于向量a、b。

假设向量a和向量b在水平地上，那么向量c，要么竖直向上，要么竖直向下。如果想具体判定向量c的朝向，最简单的方式，就是用箭头ArrowHelper可视化c，一看便知。

偏理论的方式就是通过右手螺旋定则，判断叉乘结果c的方向，没有threejs箭头简单直观，如果你不想掌握，也没关系，写代码时候，用ArrowHelper类辅助判断。

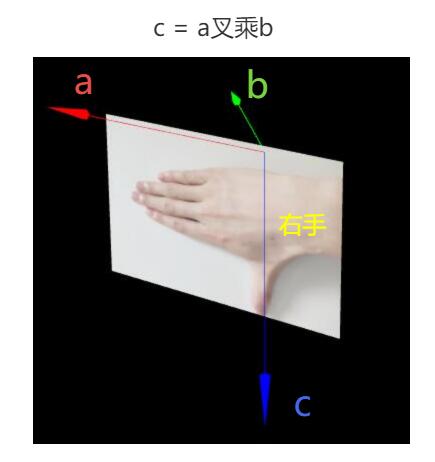
你先把向量c想象成一根筷子，尝试用手去握住它。具体过程就是，把右手手掌展平，四指并拢，大拇指与四指垂直，假设向量a和b处于水平平面上，向量c就是竖直方向，让大拇指沿着c，大拇指朝上还是朝下，随便先选个方向，让四指沿着向量a的方向，去开始握住向量c，这时候如果四指旋转的方向靠近向量b，那么说明大拇指的指向方向是向量c的方向，否则反之。

叉乘.cross()

.cross()和.crossVectors()都是向量对象的叉乘计算方法，功能一样，只是使用的细节有些不同，向量对象叉乘的结果仍然是向量对象。

const c = new THREE.Vector3();
c.crossVectors(a,b);

a.clone()克隆一个和a一样的向量，和b叉乘a.cross(b)后，作为结果c。

const c = a.clone().cross(b);