2. 模型矩阵

# 模型矩阵

在图形学中经常会提到模型矩阵的概念，其实模型矩阵就是咱们上节课介绍的平移矩阵、旋转矩阵、缩放矩阵的统称，或者说模型矩阵是平移、缩放、旋转矩阵相乘得到的复合矩阵。

假设一个顶点原始坐标(2,0,0)。

先平移2、后缩放10：如果先沿着x轴平移2，变为(4,0,0)，再x轴方向缩放10倍，最终坐标是(40,0,0)。

先缩放10、后平移2：如果先x轴方向缩放10倍，变为(20,0,0)，再沿着x轴平移2，最终坐标是(22,0,0)。

你可以发现上面同样的平移和缩放，顺序不同，变换后的顶点坐标也不相同。

假设一个顶点原始坐标(2,0,0),先沿着x轴平移2，变为(4,0,0)，再x轴方向缩放10倍，最终坐标是(40,0,0)。这个过程可以用上节课介绍的矩阵乘法运算去表示。

模型矩阵：先计算所有几何变换对应矩阵的乘积，得到一个模型矩阵，再对顶点坐标进行变换。

先把顶点几何变换对应的所有矩阵进行乘法运算，得到一个新的复合矩阵(模型矩阵)，这个模型矩阵可以用来表示顶点坐标所有的几何变换。

把上面缩放矩阵和平移矩阵的顺序调换，重新计算结果，你会发现，和上面计算的模型矩阵不同，变换后坐标也不是(40,0,0),而是(22,0,0)。

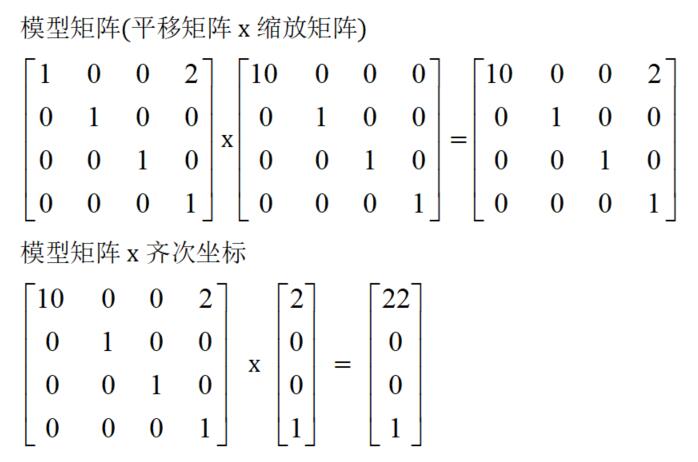
这就是告诉大家，矩阵的乘法运算，不满足交换律，矩阵顺序，不能随意设置，先发生的平移矩阵，放在后面，后发生的缩放矩阵放在前面，或者说，先发生的平移矩阵，更靠近顶点的齐次坐标。

单位矩阵就是对角线上都为1，其它为0的矩阵。

单位矩阵乘其它矩阵，或者其它矩阵成单位矩阵，新矩阵都和其它矩阵一样，不受范围矩阵影响，单位矩阵有点类似自然数加减乘除的1。